Networks and long-range mobility in cities: A study of more than one billion taxi trips in New York City

We analyze the massive data set of more than one billion taxi trips in New York City, from January 2009 to December 2015. With these records of seven years, we generate an origin-destination matrix that has information of a vast number of trips. The mobility and flow of taxis can be described as a directed weighted network that connects different zones of high demand for taxis. This network has in and out degrees that follow a stretched exponential and a power law with an exponential cutoff distributions, respectively. Using the origin-destination matrix, we obtain a rank, called "OD rank”, analogous to the page rank of Google, that gives the more relevant places in New York City in terms of taxi trips. We introduced a model that captures the local and global dynamics that agrees with the data. Considering the taxi trips as a proxy of human mobility in cities, it might be possible that the long-range mobility found for New York City would be a general feature in other large cities around the world.

Similar content being viewed by others

Mobility networks in Greater Mexico City

Article Open access 18 January 2024

The universal visitation law of human mobility

Article 26 May 2021

Exploring the mobility in the Madrid Community

Article Open access 17 January 2023

Introduction

The study and understanding of human mobility in cities is an important and challenging problem since more than half of the world population lives in urban areas 1 . Nowadays human mobility can be explored in detail thanks to the digital traces people leave on mobile/digital platforms 2,3 . Identifying global emerging patterns for human mobility is important in topics like urban planning, transport systems, the influence of the spatial distribution of a city in the mobility 4,5,6,7 , and the encounter or contact networks that emerge 8 . In addition to all these aspects lying in the field of complexity and cities, we have the science of networks with well-established tools and methods to describe complex systems 9,10,11 . In many cases, networks provide an important framework to study transportation modes and their interactions 12,13 .

Several studies have revealed that human mobility follows a long-range dynamics, akin to Lévy walks, as has been shown before as a common strategy in many animal species and humans 3,14 . In the context of networks, Lévy flights were introduced in 15 revealing that long-range displacements increase the capacity to reach efficiently to any site of the network by inducing the small-world property through the dynamics. This process has been explored in different cases as diverse as fractional diffusive transport 16,17,18,19 , the dynamics on multiplex networks 20 , human mobility 8,21 , semi-supervised learning 22 , among others 19,23,24,25,26,27 .

In this research, we analyze the spatial activity of taxis as a proxy for human mobility in urban areas. From publicly available datasets, we generate an origin-destination (OD) matrix for trips during a period of seven years from January 2009 to December 2015. We identify zones with a high demand of this service and in this way, the movement of taxis can be described as a directed weighted spatial network with nodes representing high demand zones and links defined by the number of trips between two zones. In addition, we have geographic coordinates for all the nodes and the respective distances between them; as a result, the system can be described as a spatial network 28 . With all this information, available through the analysis of trip records, we study the spatial activity of taxis as a dynamical process in this particular structure. Several authors have explored spatio-temporal patterns in the mobility of taxis in different urban areas 29,30,31 . The system of taxis in New York City has been studied with different methods; in particular, considering the complete routes followed by the taxis on the street network 32,33,34,35 .

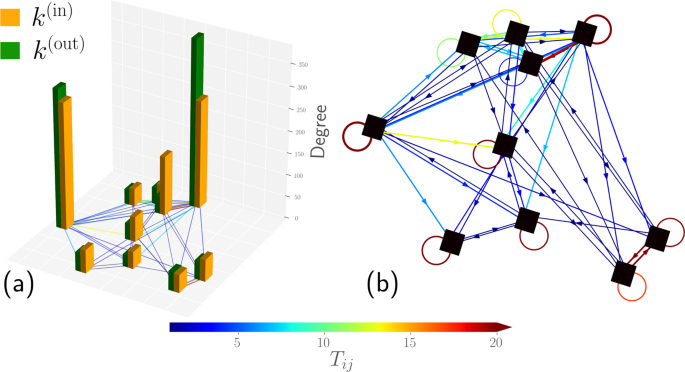
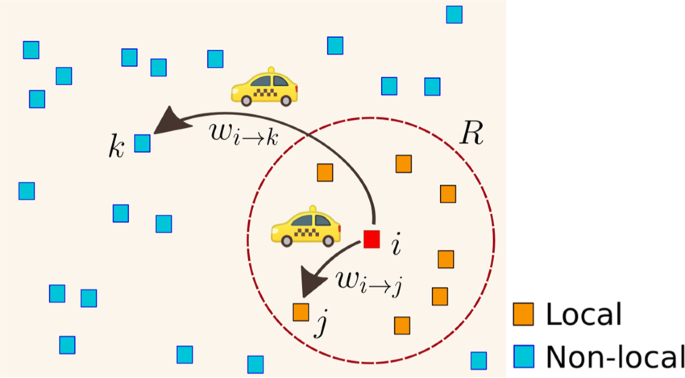
To clarify the connection between mobility and networks, let us illustrate some ideas in connection with the relation between directed weighted networks and human mobility. In Fig. 1 we depict a schematic illustration of agents moving between N = 10 specific regions denoted as squares in a two-dimensional plane. In this reduced example, we have \(<\mathscr>=1000\) trips and the values Tij (for i, j = 1, 2, …N) denote the number of trips between two regions. In Fig. 1(a) we represent with bars the values obtained for the number of trips that arrive or depart each zone; in addition, colored lines denote the number of trips Tij. In Fig. 1(b) we represent the complete structure described by the origin-destination matrix as a directed weighted network: the links have directions represented by an arrow and, with different colors in the lines, we depict the respective number of trips. Furthermore, we show with self-loops (i.e., a line connecting a zone with itself) the number of trips that start and end in the same zone, determined by the diagonal elements in the origin-destination matrix. In addition, in the study of mobility, the resulting structure is a spatial network and all the positions of the nodes are important, for instance, to determine the distance between two zones. This example shows the vast amount of information that is captured in the origin-destination matrix and its direct relation to a network, allowing us to use the full potential of network science to study mobility.

figure 1

The paper is organized as follows. In the first part, we identify high demand zones and generate origin-destination matrices describing the global activity of taxi’s flow. Then, we calculate the transition probabilities between high demand zones. We introduce a rank, called "OD rank”, analogous to the page rank of Google. We also implement a model that describes the spatial activity of taxis and verify the predictions of this model with the real data through Monte Carlo simulations. Our findings reveal a well defined mathematical structure for the spatial mobility in urban areas with a dynamics that combines local displacements with a particular type of long-range movements. The methods introduced are general and can be used as a framework for the study of different transportation systems in cities.

Results

Activity between zones with high demand

We explore taxi trip records taking into account the administrative boundaries including the five boroughs of New York City 36 . As a result, for the seven years studied, we have \(<\mathscr>=1\ 148\ 052\ 357\) taxi trips (see the Methods section for a detailed description of the datasets explored). In the following, we study this volume of data by using a grid with 500 × 500 square zones with dimensions 100 m × 100 m. Once this grid is defined, we examine the zones contained in the administrative boundaries of New York City. In Fig. 2, we present a map generated with the information of origin and destinations reported in the datasets. For each square zone defined before, we count the number of trips according to the registers of longitude and latitude of the initial and final locations of each trip for taxi registers from 2009 to 2015. The results depicted in Fig. 2 give us a first insight into the global activity of taxis. We can identify a high demand of this service in Manhattan, also the high activity in the John F. Kennedy (JFK) International Airport and how by exploring the origins of the trips we can detect some features of the street network in New York City. On the other hand, we can see in Fig. 2(b) that the destinations are less localized in specific zones observing that in the Bronx, Brooklyn and Queens boroughs the number of taxis arrivals is more uniform in comparison with the origins in Fig. 2(a). This particular feature reveals how taxi transportation manages to permeate almost all the regions of the city.

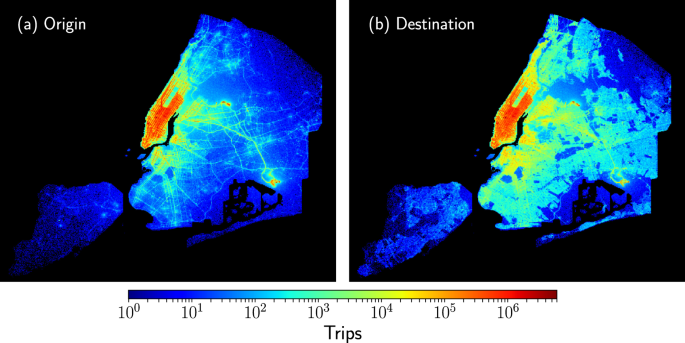
figure 2

In Fig. 2, we can identify zones in New York City with low demand for taxis or where only a reduced number of taxis arrives. Even considering the counts in seven years of activity, we can identify zones with dimensions 100 m × 100 m for which less than 10 3 taxi trips arrive or depart. This is a small number in comparison with the values of zones with a high demand for which we observe more than a million arrivals or departures. Much of these zones are located in Manhattan but also other zones of the city. In what follows, we study the flow of taxis between zones with high demand and we will describe the global spatial dynamics as a directed weighted spatial network. All the zones in our study are defined by a square with dimensions 100 m × 100 m and, for each year, we classify a region as a high activity zone if, in this specific part of the city, the number of arrivals and departures are at least 10 3 . In this way, the minimum number of arrivals at a high activity zone is at least 10 3 trips, and the same rule applies to the number of taxis leaving this region. This limit is reasonable due to the high quantity of trip records explored per year in the complete database. In addition, by using this rule we reduce possible errors produced by the inaccuracy in the origin and destination coordinates. By applying the criteria described before to the taxi trips in 2015, the number of high demand zones for this year is 4 353 and the total number of trips between these zones is \(<\mathscr>=128\ 984\ 657\) that represents a 90.22% of the original database described in the Methods section. We found similar values for the trips from 2009 to 2014. The results for the number of high demand zones N and the total number of trips \(<\mathscr>\) are presented in Table 1.

figure 3

Let us now analyze the statistical properties of the directed weighted network associated with mobility in New York City. In order to do so, we show in Fig. 4 two probability distributions: one associated to the in-degree of the network \(_^<(<\rm>)>\) (Fig. 4(a)) and the other one associated with the out-degree of the network \(_^<(<\rm>)>\) (Fig. 4(b)). We explore all the in and out-degrees, for seven years, from 2009 to 2015, in the interval 10 3 ≤ k ≤ 10 6 . With the aim of finding the best fit of the aggregated data of mobility for these distributions, we used the tools and procedures described by Clauset et al. (2009) as given in ref. 37 , that are implemented in the powerlaw package library described in references 38,39,40 . In order to decide the best fit and perform a proper statistical analysis, we explore several candidates for the distribution models: power law, power law with an exponential cutoff, exponential, stretched exponential and log-normal.

figure 4

For the statistical distributions considered, we calculate the Kolmogorov-Smirnov (KS) distance between them in a pairwise fashion. This KS distance gives us a first indicator (goodness of fit) of the proximity of the data and the proposed distribution model. Then, we compare the different distributions via a likelihood ratio test by calculating the log-likelihood function of each one of the selected distributions. The sign of this ratio gives us a criterion to discriminate between distributions (see reference 37 ). After this model selection, the best two fits were the power law with an exponential cutoff (EC), with a probability density 37 :

and the stretched exponential (SE) 37 :

where k represents the degree, \(_<\min >\) is the minimum value considered in the fit and Γ(x, y) denotes the incomplete gamma function. Notice that both distributions have two parameters, that we will distinguish with a superindex EC for the power law with an exponential cutoff, and with a superindex SE for the stretched exponential; however, we will not indicate these superindexes in Eqs. 4–5 to simplify the notation. We use λ EC and γ EC for the power law with an exponential cutoff and λ SE and β SE for the stretched exponential.

For the in-degrees in Fig. 4(a), the best fit is the stretched exponential with parameters \(_>>^>>=0.708\) and \(<\lambda >_>>^>>=4.138\times 1^\) ; in a similar way, for the power law with exponential cutoff \(<\gamma >_>>^>>=1.00000000041\) and \(<\lambda >_>>^>>=6.730\times 1^\) . On the other hand, the same analysis for the out-degrees in Fig. 4(b) concludes that the best fit is the power law with an exponential cutoff with parameters \(<\gamma >_>>^>>=1.0000000025\) and \(<\lambda >_>>^>>=6.086\times 1^\) ; in addition, for the stretched exponential \(_>>^>>=0.495\) and \(<\lambda >_>>^>>=6.834\times 1^\) .

It is surprising that both exponents \(<\gamma >_>>^>>\) and \(<\gamma >_>>^>>\) are extremely close to the value one. Thus, both distributions are well described by the power law p(k) ∝ k −1 in some range of in and out degrees.

Transition probabilities

All the information in the origin-destination matrix and in the degrees \(_^<(<\rm>)>\) and \(_^<(<\rm>)>\) allow us to analyze and understand the spatial activity of taxis as a dynamical process in a spatial directed weighted network. In this way, we can describe statistically the global dynamics of taxis in terms of transition probabilities between high demand zones of this service.

The transition probability \(_^<(<\rm>)>\) between zones i and j is defined in terms of the origin-destination matrix as:

With this definition, the transition probabilities satisfy the normalization condition:

$$\mathop\limits_^_^<(<\rm>)>=1.$$

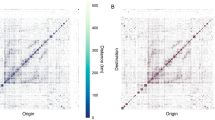
With the transition probabilities \(_^<(<\rm>)>\) , we can explore the relationship between the information in the origin-destination matrix and the matrix of distances; these matrices were presented in Fig. 3. Now, to study this connection, we calculate \(_^<(<\rm>)>\) by using the definition in Eq. 6; for each value, we have the corresponding geographical distance dij between i and j as an entry in the distance matrix D.

In Fig. 5, we depict the logarithm of the transition probability \(_^<(<\rm>)>\) as a function of the logarithm of the relation dij/d0 where d0 = 1 Km is a reference length. In Fig. 5(a), we consider all the non-null transition probabilities \(_^<(<\rm>)>\) and distances dij, for the annual data records of the taxi’s activity in 2015; we obtain a distribution of points \(\left(<<\rm<\log >>>_\left(\frac_>_>\right),<<\rm<\log >>>__^<(<\rm>)>\right)\) for all the zones with high demand (i, j = 1, 2, …, N). We show the results as a two-dimensional histogram that quantifies the frequencies of these values in hexagonal bin counts.

figure 5

Our findings in Fig. 5 reveal that the transition probabilities of taxis are approximately constant \(_^<(<\rm>)>=1^\) for distances less than a characteristic value R = 1.8 Km. In contrast, for distances greater than R, the transition probabilities are well described by a power law with an exponential cutoff relation:

$$_^<(<\rm>)>=a\frac_>^_-R)>\qquad >\qquad _ > R,$$

where continuity for dij = R requires a = 10 c . Now, to find the best fit, we analyze the pairs \(\left(<<\rm<\log >>>_\left(\frac_>_>\right),<<\rm<\log >>>__^<(<\rm>)>\right)\) presented in Fig. 5 for values 0.1 Km ≤ dij ≤ 11 Km. We divide the data considering pairs in the region dij ≤ R and dij > R with R = 1.8 Km. In Fig. 6(a) we show the statistical analysis of the values \(c=<<\rm<\log >>>__^<(<\rm>)>\) found for dij ≤ R, we see that the values c are distributed with a pronounced peak around c = −3.2, we use this value to describe the probabilities of transition. In a similar way, once defined c, we calculate β in Eq. 8 for dij > R. In Fig. 6(b), we analyze the probability density of the values β and we identify a peak around β = 0.15 Km −1 .

figure 6

The piecewise approximations described by the values R = 1.8 Km, c = −3.2 and β = 0.15 Km −1 are represented with dashed lines in Fig. 5. A similar behavior has been detected in the analysis of the transportation network of stations in bicycle sharing systems operating in New York City and Chicago 21 . In these cases, the value R ≈ 1 Km defines local displacements and the long-range dynamics is well described by \(_^<(<\rm>)>\propto _^\) . In this way, in bike-sharing systems R is reduced in comparison to our findings for taxi trips; in addition, the long-range spatial activity qualitatively has similar characteristics to those observed in Fig. 5.

OD rank

The transition matrix W (out) with elements \(_^<(<\rm>)>\) defined in Eq. 6 allow us to understand human mobility as a dynamical process in a spatial directed weighted network. Well-known results in stochastic processes apply for the transition matrix W (out) 10 . In most cases, origin-destination matrices are non-symmetric; as a consequence, it is convenient to analyze the transition matrix W (out) establishing an analogy with the Google matrix 41 , with a mathematical structure entirely general that applies to any graph or network in any domain 42 . In the following, we explore how by using this connection, the eigenvalues and eigenvectors of W (out) give valuable information to understand the movement of taxis.

The transition matrix W (out) has left and right eigenvectors. Left eigenvectors \(<\overrightarrow<\Phi >>_\) with elements ϕj(i) satisfy:

$$<\overrightarrow<\Phi >>_>>^<(<\rm>)>=<\lambda >_<\overrightarrow<\Phi >>_\qquad >\qquad j=1,2,\ldots ,N,$$

where \(<\<<\lambda >_\>>_^\) are the eigenvalues of the transition matrix. Right and left eigenvectors form an orthonormal base and have the same eigenvalues. On the other hand, the stochastic matrix W (out) fulfills Eq. 7 and, by definition, the elements of Tij satisfy Tij ≥ 0; therefore, W (out) belongs to the class of Perron-Frobenius operators with a possibly degenerate unit eigenvalue λ = 1 and other eigenvalues obeying ∣ λ ∣ ≤ 1 (see 43 for details).

In Fig. 7(a) we plot the eigenvalues of the transition matrix W (out) for taxi trips in New York City in 2015. We use the origin-destination matrix in Fig. 3(a) and the definition in Eq. 6. The results were obtained numerically and, due to the asymmetry of the origin-destination matrix, the eigenvalues are complex numbers. In Fig. 7(a) we show the real and imaginary part of each of the eigenvalues λi for i = 1, 2, …, N = 4 353. In this analysis, we found that only one eigenvalue satisfies λ = 1, a result that reveals that the directed network associated with the mobility between sites of high demand for taxis is connected. Therefore, the links in the network connect all the zones. This particular result can be interpreted using the terminology of random walks on networks. In this case, the movement of a random walker defined in terms of the transition matrix W (out) is capable to visit any node of the network only by moving on the links, independently of the initial configuration. As we mentioned before, the high connectivity observed in the origin-destination matrix is a consequence of considering high demand zones with a criterion that requires a high number of departures and arrivals in each zone avoiding the emergence of isolated parts. However, the approach developed is general and in other cases, similar spectral analysis of the transition matrix could be an important tool to identify disconnected parts in a transportation system.

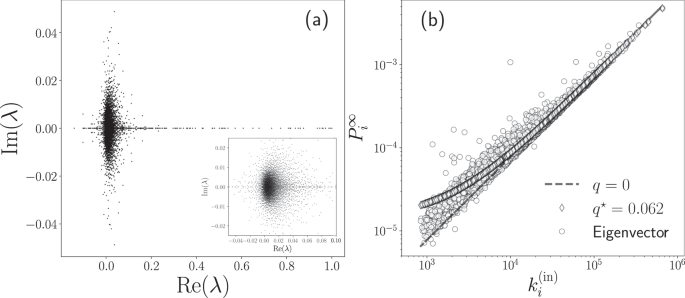
figure 7

In addition to the eigenvalues, the respective eigenvectors of the transition matrix provide valuable information about dynamical processes on networks 10,19 . In particular, the left eigenvector associated with the eigenvalue λ = 1 defines a ranking vector \(<\overrightarrow<<\bf>>>^<\infty >\) with elements \(_^<\infty >\) for i = 1, 2, …, N and satisfies \(<\overrightarrow<<\bf>>>^<\infty >>>^<(<\rm>)>=<\overrightarrow<<\bf>>>^<\infty >\) , therefore:

In the study of random walks on networks, the vector \(<\overrightarrow<<\bf>>>^<\infty >\) is the stationary probability distribution. The value \(_^<\infty >\) gives the probability of a random walker to reach the node i after a large number of steps 19 . In the context of the Google matrix, the vector \(<\overrightarrow<<\bf>>>^<\infty >\) determines the importance of a node in a network establishing a PageRank of the Web 43 . In the analysis of mobility with a transition matrix W (out) , the vector \(<\overrightarrow<<\bf>>>^<\infty >\) defines a ranking of the zones used in the definition of the origin-destination matrix. Due to this connection, we call this ranking “OD rank”.

In Fig. 7(b), we show the results obtained numerically for the OD rank \(<\overrightarrow<<\bf>>>^<\infty >\) associated with the eigenvalue λ = 1 of the transition matrix W (out) that describes the taxi’s flow in 2015. Our findings in this figure reveal a connection between the OD rank \(_^<\infty >\) of a zone i and the respective in-degree \(_^<(<\rm>)>\) . In a similar way to the findings for the PageRank algorithm for Google, the stationary probability distribution \(<\overrightarrow<<\bf>>>^<\infty >\) is a measure of the popularity of nodes that is mostly due to the in-degree dependence; in a mean-field approximation the stationary distribution of the PageRank algorithm is given by 44 :

where 0 ≤ q ≤ 1. Searching the optimal value q * that minimizes the quadratic error \(S(q)=_^<(_^<\infty >-_^<\infty >(q))>^\) , we get for the best fit:

In Fig. 7(b) we illustrate the approximation given by Eq. 11, for q = 0 and q * = 0.062, obtained for the best fit. However, Eq. 11 is a mean field result and important deviations may appear 10,44,45,46 . The result given by Eq. 11 makes sense in the description of taxis since the importance of a high demand zone can be defined in terms of the number of taxi trips k (in) that arrive at this specific location. For example, in our schematic illustration presented in Fig. 1(a), now we understand that the bars with the value k (in) determine the importance of the zones.

The transition probability matrix W (out) defined in Eq. 6 captures all the information about the system’s global activity. We think that an OD rank of the zones defined as \(<\overrightarrow<<\bf

>>>^<\infty >\) can be a valuable measure in the analysis of different transportation systems and a complement to other types of ranking algorithms introduced to determine location attractiveness incorporating geographic considerations into the PageRank algorithm 47,48,49 .

Random walk strategy

The results obtained before for the relationship of the transition probabilities describing the flow of taxis between zones and the geographical distances separating these locations, suggest that the spatial dynamics can be approximately described by a model with constant transitions to zones in a local neighborhood within a distance R, and a long-range dynamics defined by probabilities of transition proportional to \(^_-R)>_^\) . The analysis of more than a billion trips reveals a particular emergent pattern in the spatial activity. The movement of taxis between high demand zones can be classified into two types of trips with particular characteristics illustrated in Fig. 8. We have local displacements for which a taxi departs from a high demand site and the probability of moving to another site of high activity is independent of the distance that separates them if they are located at a distance less than a value R. On the other hand, there may also be long-range displacements for which the separation between origin and destinations require distances greater than R. For this type of movements, we find that the probability of having a long-range trip depends on the distance and these particular transitions have characteristics observed in truncated Lévy flights.

figure 8

In this way, to describe the global activity of the taxi’s mobility we use the model:

$$_^<(<\rm>)>(R,\beta )=\frac<<\Omega >_(R,\beta )>_^<\Omega >_(R,\beta )>,$$

In this model, β and R are positive real parameters. The transition probabilities defined in Eqs. 13 and 14 are illustrated in Fig. 8. The radius R determines a neighborhood around each zone where the trips occur with equal probability to move from the initial site to any of the high demand zones in this region. Therefore, the displacements are independent of the geographical distance between origin and destination. That is, if there are S sites inside a circle of radius R, the probability of going to any of these sites is uniform. Additionally, for places beyond the local neighborhood, for distances greater than R, the transition probability decays as a power law with an exponential cutoff of the distance and is proportional to \(^_-R)>_^\) . In this way, the parameter R defines a characteristic length of the local neighborhood and β controls the probability to have long-range displacements. In particular, in the limit β → ∞ the dynamics becomes local. We introduced a similar model with long-range transitions proportional to \(_^\) (α > 0) in reference 8 in the context of human mobility and encounter networks. In this case, the resulting dynamics can be similar to a rank model 50,51,52 and a gravity model 3,53,54,55 . It is worth mentioning that the inverse of the parameter β in Eq. 14 gives us a characteristic distance; this exponential cutoff takes into account the finite size effect associated with a finite system like New York City.

In our previous analysis in Fig. 5, we found that R ≈ 1.8 Km. This value defines what we understand as a local neighborhood for this transport system. On the other hand, for distances dij > R, the probability to have a trip to a zone is highly influenced by the geographical distance and this long-range dynamics is determined by the values \(^_-R)>_^\) with β = 0.15 Km −1 .

In the following part, we explore the predictions of this model for the annual global activity of taxi displacements in New York City by using the parameters R = 1.8 Km and β = 0.15 Km −1 found in the analysis of the taxi’s flow between high demand zones. In addition to Eqs. 13 and 14, that model the displacement between high demand zones, it is important to consider that these zones have different relevance in the whole dynamics, i.e., a trip can start from different zones with non-uniform probabilities. This fact is well described by the values of the out-degree \(_^<(<\rm>)>\) defined in Eq. 2 that gives the number of trips with origin in the zone i. In addition, from the results in Fig. 4, we know that the values \(_^<(<\rm>)>\) follow a hierarchical distribution with probabilities that decay as p(k) ∝ k −γ e −λk where k represent the values of the out-degree. This result is observed in the annual datasets from 2009-2015. In this way, we simulate the dynamics of multiple taxis that start from an initial zone chosen randomly with a probability proportional to the values \(<\<_^<(<\rm>)>\>>_^\) that quantify the importance of each zone in the city. Then, a displacement is generated randomly from the origin site to a final zone by using the transition probabilities in Eq. 13; this algorithm is repeated to generate, through Monte Carlo simulations, the same number of displacements between high demand zones, as reported in Table 1.

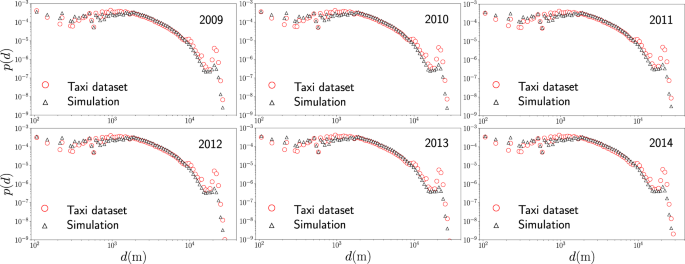
In Fig. 9 we present the statistical analysis of the taxi’s displacements d generated randomly and the real values considering the activity in New York City in 2015. In our simulation, we generate 128 984 657 random displacements following the model in Eq. 13, with β = 0.15 Km −1 and R = 1.8 Km. Our findings show an agreement between the predictions of the model and the real dynamics. However, we observe that the predictions do not agree with the real data around d = 10 Km and d = 20 Km; this is a consequence of the singular dynamics induced by the two airports in New York City. An accurate modeling capturing the effects of these very attractive sites in a city requires modifications to the model explored. This fact is also visible in Fig. 5 where, for distances around 20 Km, we see different values of the transition probability that are not described by a model with long-range trips following \(_^<(<\rm>)>\propto ^_-R)>_^\) .

figure 9

Finally, we repeat the same procedure to compare the predictions of the model with respect to the real data for taxi’s activity from 2009 to 2014. Our results for Monte Carlo simulations are presented in Fig. 10. We observe the same characteristics found in Fig. 9, with a good agreement between model and the data. The number of locations of high demand N and the number of displacements analyzed for each year are reported in detail in Table 1. The results in Table 1 also reveal that in average, in a year, approximately 43% of the trips are local movements for which the geographical distance d ≤ 1.8 Km, the rest of the trips are non-local with d > 1.8 Km.

figure 10

Discussion

In this research, we explore the massive records of more than one billion taxi-trips in New York City from January 2009 to December 2015. With this dataset of seven years, we generate an origin-destination matrix that has detail information of a vast number of trips. The mobility in New York City can be described as a directed weighted network that connects different zones of high demand for taxis. Each zone is characterized by the number of trips that arrive or depart from it and corresponds to nodes in the network. The arrivals and departures are the in-degrees and out-degrees of the directed network, and the flow gives different weights to the links of this spatial network.

We present a statistical analysis of the travel distance of each trip and found a long-range distribution that is almost the same for each of the seven years studied. On the other hand, the degree distributions, for the in and out degrees are, respectively, well modeled by a stretched exponential and a power law with an exponential cutoff. By defining the transition probabilities between zones, given by the origin-destination matrix and the out-degree, we are able to obtain a rank, called “OD rank”, analogous to the page rank of Google. We calculate the spectrum of eigenvalues and the main eigenvector, which is related to the in degree. The components of this eigenvector give the more relevant and attractive places in New York City, in terms of taxi trips.

The dependence of the transition probabilities with the distance between zones is obtained from the dataset, and based on that, we introduce a model that captures the global dynamics of trips. The data and the model describe, for short distances, a local dynamics independent of the spatial distance, and, for large distances, a dynamics that decays with distance as a power law with an exponential cutoff. The data agrees quantitatively with Monte Carlo simulations based on our model.

Finally, considering the taxi trips as a proxy of human mobility in cities, it might be possible that the long-range mobility and other features found for New York City would be rather general, and thus we expect a similar behavior in other large cities around the world for which these ideas can be applied as well.

Methods

Dataset description

In this section, we present a global description of the records explored to study the spatial dynamics in New York City. We use data for the activity of taxi trips from January 2009 to December 2015; these datasets are available to the public by the Taxi and Limousine Commission in the New York City open data website 56 . The data available include information for all taxi trips in New York City when the taxis are in service. The records comprise several fields capturing pick-up and drop-off dates and times, pick-up (origin) and drop-off (destination) locations, itemized fares, rate types, payment types and driver-reported passenger counts 56 .

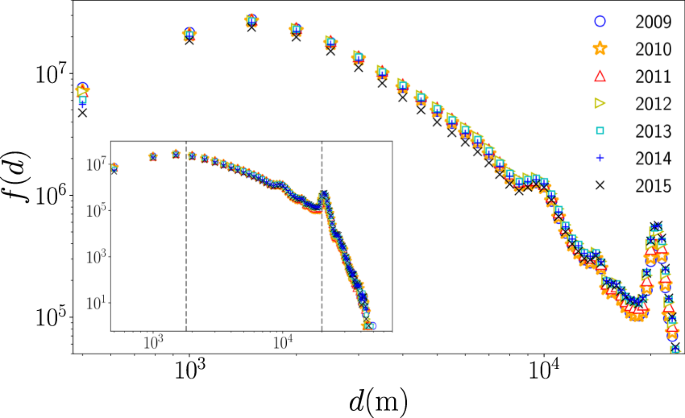
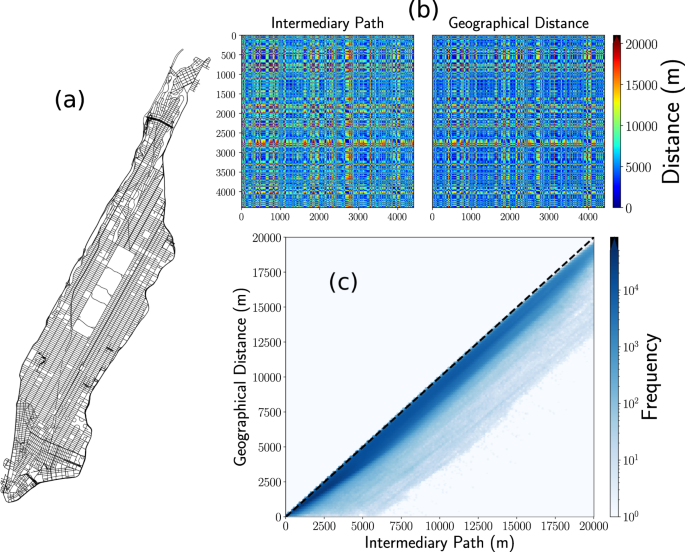
Now, to complement the information in Fig. 2, and identify other global characteristics in the taxi’s spatial activity, we analyze the geographical distance d between the origin and destinations in each trip calculated from the longitude and latitude coordinates of these locations reported in the database. Here, it is worth mentioning that other types of distances can be implemented; in particular, the distance of the path in the street network connecting origin and destinations. In fact, powerful techniques have been introduced exploring taxi trips in New York City to estimate the driving distance based on the origin and destination coordinates 59 . However, due to the different paths that a taxi can follow to carry out each trip, in the following we use the geographical distance d. In Fig. 11, we present the statistical analysis of the geographical distances d. We depict the frequencies f(d) of the displacements obtained from uniform bin counts with Δd = 500 m for taxi trips. Different markers show the results for the analysis in a year. We can see that the frequencies f(d) maintain the same characteristics from 2009 to 2015, and the statistics reveal three important intervals: the first for d < 1.8 Km with higher values of the frequencies, a second interval for 1.8 Km ≤ d < 20 Km where f(d) gradually decays and finally, for distances around 20 Km, we identify a peak that decays rapidly with the distance; this peak is associated with large displacements from Manhattan to the JFK airport (as a reference, the geographical distance between Times Square and the JFK airport is 20.6 Km). In a similar way, we identify another relative maximum at d = 10 Km: this increase in the frequencies is associated with trips between Manhattan and La Guardia airport (with d = 9.8 Km between Times Square and this airport). These are examples of how important locations can induce long-range dynamics in the taxi’s mobility. In this case, the two airports in New York City influence the taxi transportation mode in the whole city. This important feature has been observed in other cities with airports located at the city’s periphery (a particular case is reported in 31 ).

figure 11

In Table 2, we summarize the global information found for the spatial dynamics per year. We present the number of taxi trips analyzed, the average distance, the largest distance traveled as well as the fraction of trips with distances at different intervals. From the information in this table, when we examine the complete records from 2009 to 2015, we observe that 41.33% of the taxi trips have displacements with d less than 1.8 Km, whereas a 57.49% of the trips involve long-range displacements in the interval 1.8 Km ≤ d < 20 Km, and only a 1.18% of the trips have d greater than 20 Km. The average displacement of trips is \(\left\langle d\right\rangle =3.3\ >\) and the maximum value observed in the records is 51.87 Km. All these quantities give us a first characterization of the spatial activity of the taxi transportation mode.

figure 12

References

  1. Batty, M. The New Science of Cities (MIT Press, Cambridge, MA, 2013).
  2. Barthélemy, M. The Structure and Dynamics of Cities: Urban Data Analysis and Theoretical Modeling (Cambridge University Press, 2016).
  3. Barbosa, H. et al. Human mobility: Models and applications. Phys. Rep.734, 1–74 (2018). ArticleADSMathSciNetMATHGoogle Scholar
  4. Louail, T. et al. From mobile phone data to the spatial structure of cities. Sci. Rep.4, 5276 (2014). ArticleCASPubMedPubMed CentralGoogle Scholar
  5. Louail, T. et al. Uncovering the spatial structure of mobility networks. Nat. Commun.6, 6007 (2015). ArticleADSCASPubMedGoogle Scholar
  6. Lee, M. & Holme, P. Relating land use and human intra-city mobility. PLoS ONE10, e0140152 (2015). ArticlePubMedPubMed CentralCASGoogle Scholar
  7. Riascos, A. P. Universal scaling of the distribution of land in urban areas. Phys. Rev. E96, 032302 (2017). ArticleADSCASPubMedGoogle Scholar
  8. Riascos, A. P. & Mateos, J. L. Emergence of encounter networks due to human mobility. PLoS ONE12, e0184532 (2017). ArticleCASPubMedPubMed CentralGoogle Scholar
  9. Newman, M. E. J. Networks: An Introduction (Oxford University Press, Oxford, 2010).
  10. Barrat, A., Barthélemy, M. & Vespignani, A. Dynamical Processes on Complex Networks (Cambridge University Press, Cambridge, 2008).
  11. Barabási, A.-L. Network science (Cambridge University Press, Cambridge, 2016).
  12. Gallotti, R. & Barthélemy, M. Anatomy and efficiency of urban multimodal mobility. Sci. Rep.4, 6911 (2014). ArticleADSCASPubMedPubMed CentralGoogle Scholar
  13. Aleta, A., Meloni, S. & Moreno, Y. A Multilayer perspective for the analysis of urban transportation systems. Sci. Rep.7, 44359 (2017). ArticleADSPubMedPubMed CentralGoogle Scholar
  14. Boyer, D. et al. Scale-free foraging by primates emerges from their interaction with a complex environment. Proc. R. Soc. B273, 1743–1750 (2006). ArticlePubMedPubMed CentralGoogle Scholar
  15. Riascos, A. P. & Mateos, J. L. Long-range navigation on complex networks using Lévy random walks. Phys. Rev. E86, 056110 (2012). ArticleADSCASGoogle Scholar
  16. Riascos, A. P. & Mateos, J. L. Fractional dynamics on networks: Emergence of anomalous diffusion and Lévy flights. Phys. Rev. E90, 032809 (2014). ArticleADSCASGoogle Scholar
  17. de Nigris, S., Carletti, T. & Lambiotte, R. Onset of anomalous diffusion from local motion rules. Phys. Rev. E95, 022113 (2017). ArticleADSPubMedGoogle Scholar
  18. Michelitsch, T. M., Collet, B. A., Riascos, A. P., Nowakowski, A. F. & Nicolleau, F. C. G. A. Fractional random walk lattice dynamics. J. Phys. A: Math. Theor50, 055003 (2017). ArticleADSMathSciNetMATHGoogle Scholar
  19. Michelitsch, T. M., Riascos, A. P., Collet, B. A., Nowakowski, A. F. & Nicolleau, F. C. G. A. Fractional Dynamics on Networks and Lattices (ISTE/Wiley, London, 2019).
  20. Guo, Q., Cozzo, E., Zheng, Z. & Moreno, Y. Lévy random walks on multiplex networks. Sci. Rep.6, 37641 (2016). ArticleADSCASPubMedPubMed CentralGoogle Scholar
  21. Loaiza-Monsalve, D. & Riascos, A. P. Human mobility in bike-sharing systems: Structure of local and non-local dynamics. PLoS ONE14, e0213106 (2019). ArticleCASPubMedPubMed CentralGoogle Scholar
  22. de Nigris, S., Bautista, E., Abry, P., Avrachenkov, K. & Goncalves, P. Fractional graph-based semi-supervised learning. In 2017 25th European Signal Processing Conference (EUSIPCO), 356–360 (2017).
  23. Zhao, Y., Weng, T. & Huang, D. Lévy walk in complex networks: An efficient way of mobility. Physica A: Stat. Mech. Appl.396, 212–223 (2014). ArticleADSGoogle Scholar
  24. Weng, T., Small, M., Zhang, J. & Hui, P. Lévy walk navigation in complex networks: A distinct relation between optimal transport exponent and network dimension. Sci. Rep.5, 17309 (2015). ArticleADSPubMedPubMed CentralCASGoogle Scholar
  25. Weng, T. et al. Navigation by anomalous random walks on complex networks. Sci. Rep.6, 37547 (2016). ArticleADSCASPubMedPubMed CentralGoogle Scholar
  26. Estrada, E. et al. Random multi-hopper model: super-fast random walks on graphs. J. Compl. Net.6, 382–403 (2018). ArticleMathSciNetGoogle Scholar
  27. Riascos, A. P., Michelitsch, T. M., Collet, B. A., Nowakowski, A. F. & Nicolleau, F. C. G. A. Random walks with long-range steps generated by functions of laplacian matrices. Theory Exp.2018, 043404 (2018). MathSciNetGoogle Scholar
  28. Barthélemy, M. Spatial networks. Phys. Rep.499, 1–101 (2011). ArticleADSMathSciNetCASGoogle Scholar
  29. Veloso, M., Phithakkitnukoon, S. & Bento, C. Urban mobility study using taxi traces. In Proceedings of the 2011 International Workshop on Trajectory Data Mining and Analysis, TDMA 11, 23–30 (ACM, New York, NY, USA, 2011).
  30. Hoque, M. A., Hong, X. & Dixon, B. Analysis of mobility patterns for urban taxi cabs. In 2012 International Conference on Computing, Networking and Communications (ICNC), 756–760 (2012).
  31. Wu, L., Zhi, Y., Sui, Z. & Liu, Y. Intra-urban human mobility and activity transition: Evidence from social media check-in data. PLoS One9, e97010 (2014). ArticleADSPubMedPubMed CentralCASGoogle Scholar
  32. Santi, P. et al. Quantifying the benefits of vehicle pooling with shareability networks. Proc. Natl. Acad. Sci. USA111, 13290–13294 (2014). ArticleADSCASPubMedPubMed CentralGoogle Scholar
  33. Tachet, R. et al. Scaling law of urban ride sharing. Sci. Rep.7, 42868 (2017). ArticleADSCASPubMedPubMed CentralGoogle Scholar
  34. Vazifeh, M. M., Santi, P., Resta, G., Strogatz, S. H. & Ratti, C. Addressing the minimum fleet problem in on-demand urban mobility. Nature557, 534–538 (2018). ArticleADSCASPubMedGoogle Scholar
  35. O’Keeffe, K. P., Anjomshoaa, A., Strogatz, S. H., Santi, P. & Ratti, C. Quantifying the sensing power of vehicle fleets. PNAS116, 12752–12757 (2019). ArticleADSPubMedCASPubMed CentralGoogle Scholar
  36. NYC borough boundaries, https://data.cityofnewyork.us/City-Government/Borough-Boundaries/tqmj-j8zm.
  37. Clauset, A., Shalizi, C. R. & Newman, M. E. J. Power-law distributions in empirical data. SIAM Rev.51, 661–703 (2009). ArticleADSMathSciNetMATHGoogle Scholar
  38. Klaus, A., Yu, S. & Plenz, D. Statistical analyses support power law distributions found in neuronal avalanches. PLoS One6, e19779 (2011). ArticleADSCASPubMedPubMed CentralGoogle Scholar
  39. Alstott, J., Bullmore, E. & Plenz, D. Powerlaw: A python package for analysis of heavy-tailed distributions. PLoS One9, e85777 (2014). ArticleADSPubMedPubMed CentralCASGoogle Scholar
  40. powerlaw: A Python Package for Analysis of Heavy-Tailed Distributions, https://pypi.org/project/powerlaw/.
  41. Brin, S. & Page, L. The anatomy of a large-scale hypertextual web search engine. Comput. Netw. ISDN Syst30, 107–117 (1998). ArticleGoogle Scholar
  42. Gleich, D. Pagerank beyond the web. SIAM Rev.57, 321–363 (2015). ArticleMathSciNetMATHGoogle Scholar
  43. Ermann, L., Frahm, K. M. & Shepelyansky, D. L. Google matrix analysis of directed networks. Rev. Mod. Phys.87, 1261–1310 (2015). ArticleADSGoogle Scholar
  44. Fortunato, S., Boguñá, M., Flammini, A. & Menczer, F. Approximating pagerank from in-degree. In Aiello, W., Broder, A., Janssen, J. & Milios, E. (eds.) Algorithms and Models for the Web-Graph, 59–71 (Springer Berlin Heidelberg, Berlin, Heidelberg, 2008).
  45. Fortunato, S., Flammini, A., Menczer, F. & Vespignani, A. Topical interests and the mitigation of search engine bias. PNAS103, 12684–12689 (2006). ArticleADSCASPubMedPubMed CentralGoogle Scholar
  46. Litvak, N., Scheinhardt, W. R. W. & Volkovich, Y. Probabilistic relation between in-degree and pagerank. In Aiello, W., Broder, A., Janssen, J. & Milios, E. (eds.) Algorithms and Models for the Web-Graph, 72–83 (Springer Berlin Heidelberg, Berlin, Heidelberg, 2008).
  47. Zhong, C., Arisona, S. M., Huang, X., Batty, M. & Schmitt, G. Detecting the dynamics of urban structure through spatial network analysis. Int. J. Geogr. Inf. Sci.28, 2178–2199 (2014). ArticleGoogle Scholar
  48. Chin, W.-C.-B. & Wen, T.-H. Geographically modified pagerank algorithms: Identifying the spatial concentration of human movement in a geospatial network. PLoS One10, e0139509 (2015). ArticlePubMedPubMed CentralCASGoogle Scholar
  49. Huang, C.-Y., Chin, W.-C.-B., Wen, T.-H., Fu, Y.-H. & Tsai, Y.-S. Epirank: Modeling bidirectional disease spread in asymmetric commuting networks. Sci. Rep.9, 5415 (2019). ArticleADSPubMedPubMed CentralCASGoogle Scholar
  50. Liben-Nowell, D., Novak, J., Kumar, R., Raghavan, P. & Tomkins, A. Geographic routing in social networks. Proc. Natl. Acad. Sci. USA102, 11623–11628 (2005). ArticleADSCASPubMedPubMed CentralGoogle Scholar
  51. Noulas, A., Scellato, S., Lambiotte, R., Pontil, M. & Mascolo, C. A tale of many cities: Universal patterns in human urban mobility. PLoS One7, e37027 (2012). ArticleADSCASPubMedPubMed CentralGoogle Scholar
  52. Pan, W., Ghoshal, G., Krumme, C., Cebrian, M. & Pentland, A. Urban characteristics attributable to density-driven tie formation. Nat. Commun.4, 1961 (2013). ArticleADSPubMedCASGoogle Scholar
  53. Simini, F., González, M. C., Maritan, A. & Barabási, A.-L. A universal model for mobility and migration patterns. Nature484, 96–100 (2012). ArticleADSCASPubMedGoogle Scholar
  54. Yang, Y., Herrera, C., Eagle, N. & González, M. C. Limits of predictability in commuting flows in the absence of data for calibration. Sci. Rep.4, 5662 (2014). ArticleADSCASPubMedPubMed CentralGoogle Scholar
  55. Lenormand, M., Bassolas, A. & Ramasco, J. J. Systematic comparison of trip distribution laws and models. J. Transp. Geogr.51, 158–169 (2016). ArticleGoogle Scholar
  56. NYC Data, https://opendata.cityofnewyork.us/.
  57. Boeing, G. Osmnx: New methods for acquiring, constructing, analyzing, and visualizing complex street networks. Comput Environ Urban Syst65, 126–139 (2017). ArticleGoogle Scholar
  58. OSMnx Python Package, https://pypi.org/project/osmnx/.
  59. Sagarra, O., Szell, M., Santi, P., Díaz-Guilera, A. & Ratti, C. Supersampling and network reconstruction of urban mobility. PLoS One10, e0134508 (2015). ArticlePubMedPubMed CentralCASGoogle Scholar
  60. OpenStreetMap contributors, https://www.openstreetmap.org.

Acknowledgements

This work was supported by PAPIIT-UNAM grant No. IN116220.